♪♥ この教材は，高校数学の基本問題のうち，２次不等式のバックアップファイルです． ♫♣ 元の教材が機器や通信トラブルで読めないときに，こちらを使ってください．なお，学習の記録は付いていません． 【目次】 • ２次不等式(D>0) • ２次不等式(D=0) • ２次不等式(D<0) • ２次不等式（解き方まとめ） • ２次不等式（絶対値付き） • ２次不等式（文字係数） == ２次不等式 == ２次関数のグラフが軸と２点で交わる場合 ○　初めに2次関数のグラフが谷形になるものについて考えます。 において２次の係数が正であるとき、グラフは谷形になります。 ⇒　（ただし、）は谷形 ○　　２次不等式 　（ただし，） は，の値がの値に等しいグラフ，すなわち 　（） のグラフを利用して解くことができます． （）のグラフでは の値は座標に等しいので， となるようなの値の範囲は となるようなの値の範囲となります．（図の赤で示した部分） と軸がで交わるとき （すなわちが負）となるのは のときです． 右上に続く↑

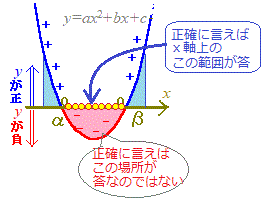
→続き ※２次不等式の解き方を身に付けるためには，まず第１に，思い込みを捨てることが重要です． ○すなわち，これまでに習った１次不等式の解き方では のように,問題文の不等号の向きと解の不等号の向きが対応しています．の係数が負の場合は，逆向きになりますが，それでも対応しています． ○これに対して， のような２次不等式では，問題文の不等号がであるからといって，解の不等号の向きが ， となるのではなく，２次関数のグラフからの符号が負になるようなの範囲を探すことになります． ではの符号が正になるようなの範囲を探すことになります．

※ここが核心※ 不等式で求めているのはの値の範囲ではなく、の値の範囲です。（この式の変数はだけ） ここで２次関数を考えると、右辺は上の不等式の左辺の値となっています。 したがって、２次関数のの値は上の不等式の左辺の値になります。 そこで、２次関数のグラフを利用して、「の値（符号）が負になる」ような「の値の範囲」を求めるということです。 　同様にして も解けます． 右上に続く↑

→続き 《要約》 の解が のとき 問題がなら， 答は マイナスは「間」 問題がなら， 答は プラスは「両側」 問題がなら， 答は マイナスは「間」 等号付き 問題がなら， 答は プラスは「両側」 等号付き

［例１］ ２次不等式x2−x−12<0を解け。 （答案） ２次方程式x2−x−12=0を解くと (x+3)(x−4)=0より x=−3, 4 「２次不等式の問題なのに」問われていない「２次方程式」について演説を始めることが重要 ２次関数y=x2−x−12のグラフは 「２次不等式の問題なのに」問われていない「２次関数」を描くことが重要 グラフを描くためには、上で求めたｘ軸との交点の座標が必要になる･･･この問題を解くためには、頂点の座標などの正確な情報は不要。 グラフから、y<0すなわち ２次不等式x2−x−12<0を満たすxの値の範囲は−3<x<4…（答） ここでようやく「２次不等式」の話に戻る。 マイナスになるのは「間（サンドイッチ）」が答

［例２］ ２次不等式x2−x−12≧0を解け。 （答案） ２次方程式x2−x−12=0を解くと x=−3, 4 ２次関数y=x2−x−12のグラフは グラフから、y≧0すなわち ２次不等式x2−x−12≧0を満たすxの値の範囲は x≦−3 , 4≦x…（答） 　論理的に同じ内容を表していれば、次にように書いてもよい。 x≦−3 , x≧4 　筆者は、小さいものから大きいものへ左から順に並べていく書き方が「分かりやすく」「間違いにくい」と考える。 　例１と同様に、「不等式の問題を解くためには２次関数のグラフが必要、２次関数のグラフを描くためには２次方程式の解が必要」と考える。 　したがって、問われていなくても「２次方程式」→「２次関数」→「２次不等式」の順に述べることが重要。 プラスになるのは「両側」が答 ※　問題に等号が付いているから、答にも等号を付ける。 よくある＃とんでもない答案＃ この問題の答を4≦x≦−3と書いてはいけない。 （4が−3よりも小さいということはない。そもそも、4≦xとx≦−3の両方を満たすようなxはなく、この問題の答となるxは２つの部分に分かれている。） 　一般に、「両側」形の範囲は、α≦x≦βの形にはまとめられない。

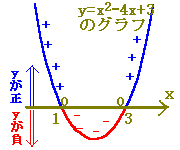
【問題】 グラフを参考にして，２次不等式の解を選びなさい． （右から正しい選択肢をクリック） (1)	2次不等式 x2−4x+3<0 の解は 1<x, 3<x x<1, x<3 1<x<3 x<1, 3<x	x2−4x+3が ０よりも小さくなる（＜）ようなxの値の範囲をさがします． ⇒　マイナスは「間」 1<x<3
(2)	2次不等式 x2+5x+6>0の解は −3<x, −2<x x<−3, x<−2 −3<x<−2 x<−3, −2<x	x2+5x+6が ０よりも大きくなる（＞）ようなxの値の範囲をさがします． ⇒　プラスは「両側」 x<−3, −2<x
(3)	2次不等式 x2−4≧0の解は x≧±2 x≦±2 −2≦x≦2 x≦−2, 2≦x	x2−4が０以上になる（≧）ようなxの値の範囲をさがします． ⇒　プラスは「両側」 （等号付き） x≦−2, 2≦x
(4)	2次不等式 x2−3x+2≦0の解は x≧1, x≧2 x≦1, x≦2 1≦x≦2 x≦1, 2≦x	ｘ2－３ｘ＋２が０以下になる（≦）ようなxの値の範囲をさがします． ⇒　マイナスは「間」 （＝付き） 1≦x≦2

(5)	2次不等式 x2≦9の解は x≧±3 x≦±3 −3≦x≦3 x≦−3, 3≦x	x2≦9の見かけに引きずられて、x≦±3と答える答案が多いが、それは間違い。 　あくまで、方程式x2=9すなわちx2−9=0の解x=±3の「間」を答えること。 −3≦x≦3
(6)	2次不等式 x2−x−1≦0の解は	２次方程式x2−x−1=0の左辺は（整数の範囲では）因数分解できないから、この方程式は解の公式を使って解く。 x2−x−1=0の解は 方程式の２つの解の「間」を不等式の解とする（等号付きで）
(7)	2次不等式 x2−2>0の解は	２次方程式x2−2=0の左辺は（整数の範囲では）因数分解できないから、この方程式は解の公式を使って解く。 x2−2=0の解は 方程式の２つの解の「両側」を不等式の解とする
(8) このページの内容について，質問や間違いの指摘があるときは，下の「コメントを投稿」という文字をクリックしてください（↓↓）	2次不等式 2x2−4x+1≦0の解は	２次方程式2x2−4x+1=0の左辺は（整数の範囲では）因数分解できないから、この方程式は解の公式を使って解く。 2x2−4x+1=0の解は 方程式の２つの解の「間」を不等式の解とする（等号付きで）