高校数学・２次不等式

2次不等式

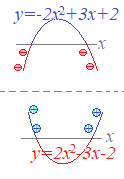
♪♥ この教材は，高校数学の基本問題のうち，２次不等式（解き方まとめ）のバックアップファイルです．
♫♣ 元の教材が機器や通信トラブルで読めないときに，こちらを使ってください．なお，学習の記録は付いていません．

【目次】 • ２次不等式(D>0) • ２次不等式(D=0)
• ２次不等式(D<0) • ２次不等式（解き方まとめ） • ２次不等式（絶対値付き） • ２次不等式（文字係数）

== ２次不等式 ==（解き方まとめ）
（Ⅰ）　初めに $x^2$ の係数が負になっている2次不等式は，両辺に－１を掛けて， $x^2$ の係数が正になるように書き換えます．

$x^2$ の係数が負になっている2次不等式，例えば
$-2x^2+ 3x+ 2\lt 0$
のような問題を「そのまま解こうとすると」
$y=-2x^2+ 3x+ 2$
という上に凸のグラフを描いて， $y\lt 0$ になるような $x$ の値の範囲を探さなければならないことになります．

このような問題は，元の不等式を
$2x^2-3x-2\gt 0$
に変形してから解くことに決めておくと，常に $x^2$ の係数が正の
$y=2x^2-3x-2$
という「よく見慣れた」グラフで解けるようになります．

そこで，以下においては $x^2$ の係数が負になっている2次不等式が登場したら，両辺に－１を掛けて， $x^2$ の係数が正になるように書き換えて解くことにします．

$y=ax^2+ bx+ c$ において２次の係数 $a$ が正であるとき、グラフは谷形になります。
⇒　 $y=ax^2+ bx+ c$ （ただし、 $a\gt 0$ ）は谷形

右上に続く↑

（Ⅱ） $x^2$ の係数が正で

ア） $ax^2+ bx+ c=0$ の解が $x=\alpha,\beta\hspace{5}(\alpha\lt\beta)$ のとき

(1) 問題が $ax^2+ bx+ c$ $\lt 0$ $\hspace{5}(a\gt 0)$ なら，

答は $\alpha$ $\lt x\lt$ $\beta$
マイナスは「間」

(2) 問題が $ax^2+ bx+ c$ $\gt 0$ $\hspace{5}(a\gt 0)$ なら，

答は $x\lt$ $\alpha,\hspace{5}\beta$ $\lt x$
プラスは「両側」

(3) 問題が $ax^2+ bx+ c$ $\underline{\le}0$ $\hspace{5}(a\gt 0)$ なら，

答は $\alpha$ $\underline{\le}x\underline{\le}$ $\beta$
マイナスは「間」
等号付き

(4) 問題が $ax^2+ bx+ c$ $\underline{\ge}0$ $\hspace{5}(a\gt 0)$ なら，

答は $x\underline{\le}$ $\alpha,\hspace{5}\beta$ $\underline{\le}x$
プラスは「両側」
等号付き

イ） $ax^2+ bx+ c=0$ の解が $x=\alpha$ （重解）のとき
（ $D=b^2-4ac=0$ のとき）

(1) 問題が $ax^2+ bx+ c$ $\lt 0$ $\hspace{5}(a\gt 0)$ なら，

答は
解なし

(2) 問題が $ax^2+ bx+ c$ $\gt 0$ $\hspace{5}(a\gt 0)$ なら，

答は $x\lt\alpha,\hspace{5}\alpha\lt x$
（ $x\ne \alpha$ でもよい）

(3) 問題が $ax^2+ bx+ c$ $\underline{\le}0$ $\hspace{5}(a\gt 0)$ なら，

答は $x=\alpha$

(4) 問題が $ax^2+ bx+ c$ $\underline{\ge}0$ $\hspace{5}(a\gt 0)$ なら，

答は「すべての実数」

ウ） $ax^2+ bx+ c=0$ が実数解をもたないとき
（ $D=b^2-4ac\lt 0$ のとき）

(1) 問題が $ax^2+ bx+ c$ $\lt 0$ $\hspace{5}(a\gt 0)$ なら，

答は
解なし

(2) 問題が $ax^2+ bx+ c$ $\gt 0$ $\hspace{5}(a\gt 0)$ なら，

答は
すべての実数

(3) 問題が $ax^2+ bx+ c$ $\underline{\le}0$ $\hspace{5}(a\gt 0)$ なら，

答は
解なし

(4) 問題が $ax^2+ bx+ c$ $\underline{\ge}0$ $\hspace{5}(a\gt 0)$ なら，

答は
すべての実数

【例題１】
２次不等式 $-2x^2+ 3x+ 2\gt 0$ の解を求めてください．

（解答）

（Ⅰ）により， $x^2$ の係数が負のときは，両辺に－１を掛けて，問題を書き換えます．

両辺に－１を掛けると
$2x^2-3x-2\lt 0$
この２次不等式を解くことにする．

まず２次方程式を解く．
因数分解できる問題は，因数分解で解くのが楽

$2x^2-3x-2=0$
の解は
$(2x+ 1)(x-2)=0$
より
$x=-\frac{1}{2},\hspace{5}2$

2次関数
$y=2x^2-3x-2$
のグラフは右図のようになるから
$y=2x^2-3x-2\lt 0$
となる $x$ の値の範囲は
$-\frac{1}{2}\lt x \lt2$ …（答）

【例題２】
２次不等式 $x(2x-1)\gt x^2+ x-3$ の解を求めてください．

（解答）

両辺に式があるときは，展開整理して左辺に集めます

$2x^2-x\gt x^2+ x-3$
$x^2-2x+ 3\gt 0$
この２次不等式を解くことにする．

まず２次方程式を解くと虚数解になるのを見たら，判別式の話にしてしまう．
$ax^2 + 2b\apos x+ c=0$
のときは
$D\apos=b\apos^2-ac$
を使うと
$D=b^2-4ac$
よりも小さな数字で調べられる

$x^2-2x+ 3=0$
の判別式は
$D\apos=1^2-3$
$=-2\lt 0$
だから
2次関数
$y=x^2-2x+ 3$
のグラフは右図のようになる

$y=x^2-2x+ 3\gt 0$
となる $x$ の値の範囲は

すべての実数…（答）

■参考･･･平方完成による不等式の証明

上記のイ） $D=0$ の場合，およびウ） $D$ の場合は，平方完成の変形により解くべき２次不等式に代えて絶対不等式の証明で行うことができますが，後に述べる事情(*)から基本練習としてはお勧めしません．

【例１】イ） $D=0$ の場合

(1)　２次不等式 $x^2-4x+ 4\lt 0$ …(A)の解を求めるとき

$x^2-4x+ 4=(x-2)^2\underline{\ge}0$ …(B)
だから
(A)は成り立たない．したがって，「解なし」…（答）

(2)　２次不等式 $x^2-4x+ 4\underline{\le} 0$ …(A)の解を求めるとき

$x^2-4x+ 4=(x-2)^2\underline{\ge}0$ …(B)
だから
$x=2$ …（答）

(*)
(1)(2)の問題において，(A)は解くべき式，(B)はつねに成り立つ式であるが，同じような不等式で書かれているためか，(B)を使って(A)を解くという関係がなかなか理解しづらい生徒が多く，教科書などでは２次関数のグラフを使った解き方が多い．

【例２】ウ） $D\lt 0$ の場合

(3)　２次不等式 $x^2-4x+ 5\gt 0$ …(A)の解を求めるとき

$x^2-4x+ 5=(x-2)^2+ 1\gt 0$ …(B)
だから
(A)はつねに成り立つ．したがって，「すべての実数」…（答）

(4)　２次不等式 $x^2-4x+ 5\underline{\le} 0$ …(A)の解を求めるとき

$x^2-4x+ 5=(x-2)^2+ 1\gt 0$ …(B)
だから
(A)は成り立たない．したがって，「解なし」…（答）

【問題1】
次の２次不等式を解きなさい．
（正しい選択肢をクリック）

(1)
$x^2-7x+ 10\lt 0$

解説やり直す

$x\lt 2,\hspace{5}5\lt x$ $2\lt x\lt 5$

解なしすべての実数

$x^2-7x+ 10=0$
$(x-2)(x-5)=0$
の解は
$x=2,\hspace{5}5$

2次関数
$y=x^2-7x+ 10$
のグラフは右図のようになるから，元の２次不等式の解は
$2\lt x \lt5$ …（答）

→閉じる←

(2)
$2x^2-4x+ 1\underline{\le} 0$

解説やり直す

$\frac{2-\sqrt{2}}{2}\underline{\le}x\underline{\le}\frac{2+\sqrt{2}}{2}$ $x\underline{\le}\frac{2-\sqrt{2}}{2},\hspace{5}\frac{2+\sqrt{2}}{2}\underline{\le}x$

$x\underline{\le}\frac{2\pm\sqrt{2}}{2}$ 解なしすべての実数

$2x^2-4x+ 1=0$
を解の公式を使って解くと
$x=\frac{2\pm\sqrt{2}}{2}$

2次関数
$y=2x^2-4x+ 1$
のグラフは右図のようになるから，元の２次不等式の解は
$\frac{2-\sqrt{2}}{2}\underline{\le}x\underline{\le}\frac{2+\sqrt{2}}{2}$ …（答）

→閉じる←

(3)
$2x^2-6x\gt 0$

解説やり直す

$x\gt 3$ $x\lt 0,\hspace{5}3\lt x$

$0\lt x\lt 3$ 解なしすべての実数

$2x^2-6x\gt 0$
$2x(x-3)=0$
の解は
$x=0,\hspace{5}3$

2次関数
$y=2x^2-6x$
のグラフは右図のようになるから，元の２次不等式の解は
$x\lt 0,\hspace{5}3\lt x$ …（答）

→閉じる←

(4)
$x^2+ 4x+ 4\underline{\le}0$

解説やり直す

$x\underline{\le}-2$ $x=-2$ $x\lt -2,\hspace{5}-2\lt x$

解なしすべての実数

$x^2+ 4x+ 4=0$
$(x+ 2)^2=0$
の解は
$x=-2$ （重解）

2次関数
$y=x^2+ 4x+ 4$
のグラフは右図のようになるから，元の２次不等式の解は
$x=-2$ …（答）

→閉じる←

【問題２】

(1)
$x^2-2x+ 2\gt 0$

解説やり直す

$x\gt 1$ $1-i\lt x\lt 1+ i$ $x\lt 1-i,\hspace{5}1+ i\lt x$

解なしすべての実数

$x^2-2x+ 2=0$
の判別式は
$D\apos=1-2=-1\lt 0$

2次関数
$y=x^2-2x+ 2$
のグラフは右図のようになるから，元の２次不等式の解は
すべての実数…（答）
※複素数には大小関係を考えないので， $1-i\lt x\lt 1+ i$ ， $x\lt 1-i,\hspace{5}1+ i\lt x$ を選んだ人は要注意です

→閉じる←

(2)
$3x^2-11x-4\lt 0$

解説やり直す

$-\frac{1}{3}\lt x\lt 4$ $x\lt -\frac{1}{3},\hspace{5}4\lt x$

解なしすべての実数

$3x^2-11x-4=0$
$(3x+ 1)(x-4)=0$
の解は
$x=-\frac{1}{3},\hspace{5}4$

2次関数
$y=3x^2-11x-4$
のグラフは右図のようになるから，元の２次不等式の解は
$-\frac{1}{3}\lt x\lt 4$ …（答）

→閉じる←

(3)
$x^2\underline{\ge}4x$

解説やり直す

$x\underline{\ge}4$ $x\underline{\le}0,\hspace{5}4\underline{\le}x$ $0\underline{\le}x\underline{\le}4$

解なしすべての実数

２次不等式を
$x^2-4x\underline{\ge}0$
の形で解く
$x^2-4x=0$
$x(x-4)=0$
の解は
$x=0,\hspace{5}4$

2次関数
$y=x^2-4x$
のグラフは右図のようになるから，元の２次不等式の解は
$x\underline{\le}0,\hspace{5}4\underline{\le}x$ …（答）

→閉じる←

(4)
$x^2+ 4x+ 8\underline{\le}0$

解説やり直す

$x\underline{\le}-4$ $-2-2i\underline{\le}x\underline{\le}-2+ 2i$

$x\underline{\le}-2-2i,\hspace{5}-2+ 2i\underline{\le}x$

解なしすべての実数

$x^2+ 4x+ 8=0$
の判別式は
$D\apos=2^2-8=-4\lt 0$

2次関数
$y=x^2+ 4x+ 8$
のグラフは右図のようになるから，元の２次不等式の解は
解なし…（答）
※複素数には大小関係を考えないので， $-2-2i\underline{\le}x\underline{\le}-2+ 2i$ ， $x\underline{\le}-2-2i,\hspace{5}-2+ 2i\underline{\le}x$ を選んだ人は要注意です

→閉じる←

【問題３】

(1)
$12(x-1)\underline{\ge}3x^2$

解説やり直す

$x\underline{\le}2$ $x\underline{\ge}2$ $x=2$

解なしすべての実数

両辺を３で割る
$4(x-1)\underline{\ge}x^2$
右辺に移項して左辺と右辺を入れ換える
$x^2-4x+ 4\underline{\le}0$
２次方程式
$x^2-4x+ 4=0$
$(x-2)^2=0$
の解は
$x=2$ （重解）

2次関数
$y=x^2-4x+ 4$
のグラフは右図のようになるから，元の２次不等式の解は
$x=2$ …（答）

→閉じる←

(2)
$7+ 20x\lt 3x^2$

解説やり直す

$x\lt -\frac{1}{3},\hspace{5}7\lt x$ $x\lt \frac{1}{3},\hspace{5}7\lt x$ $\frac{1}{3}\lt x\lt 7$

解なしすべての実数

式を左辺に移項して，両辺に－１を掛ける
$-3x^2+ 20x+ 7\lt 0$
$3x^2-20x-7\gt 0$ ←（この問題を解く）
２次方程式
$3x^2-20x-7=0$
$(3x+ 1)(x-7)=0$
の解は
$x=-\frac{1}{3},\hspace{5}7$

2次関数
$y=x^2-20x-7$
のグラフは右図のようになるから，元の２次不等式の解は
$x\lt -\frac{1}{3},\hspace{5}7\lt x$ …（答）

→閉じる←

(3)
$\frac{x^2+ x}{5}\gt\frac{x-1}{3}$

解説やり直す

$x\lt\frac{1-\sqrt{14}i}{3},\hspace{5}\frac{1+\sqrt{14}i}{3}\lt x$ $\frac{1-\sqrt{14}i}{3}\lt x\lt\frac{1+\sqrt{14}i}{3}$

解なしすべての実数

分母を払い左辺に移項する
$3x^2+ 3x\gt 5x-5$
$3x^2-2x+ 5\gt 0$
２次方程式
$3x^2-2x+ 5=0$
の判別式は
$D\apos=1^2-15=-14\lt 0$

2次関数
$y=3x^2-2x+ 5$
のグラフは右図のようになるから，元の２次不等式の解は
すべての実数…（答）

→閉じる←

(4)
$x^2+(x-1)^2\underline{\le}3$

解説やり直す

$\frac{1-\sqrt{3}}{2}\underline{\le} x\underline{\le}\frac{1+\sqrt{3}}{2}$ $\frac{1-\sqrt{5}}{2}\underline{\le} x\underline{\le}\frac{1+\sqrt{5}}{2}$

解なしすべての実数

$2x^2-2x-2\underline{\le}0$
$x^2-x-1\underline{\le}0$
２次方程式
$x^2-x-1=0$
の解は
$x=\frac{1\pm\sqrt{5}}{2}$

2次関数
$y=x^2-x-1$
のグラフは右図のようになるから，元の２次不等式の解は
$\frac{1-\sqrt{5}}{2}\underline{\le} x\underline{\le}\frac{1+\sqrt{5}}{2}$ …（答）

→閉じる←

コメント